Üstünlük stratejisi ile oyunlar m x 2 ve 2 x n boyuta indirgenirse bu oyunlar grafik yöntemiyle çözülebilir.

Örnek 6 : A ve B oyuncuları arasında oynanan (2x4) boyutlu oyunun matrisi verilmiştir. Buna göre oyunu grafik yöntemine göre çözünüz.

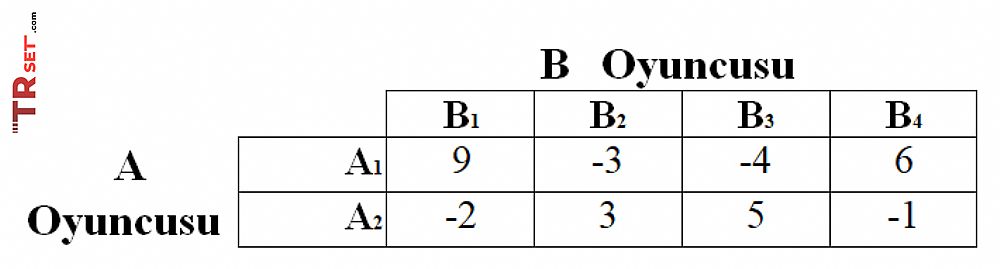
Oyun matrisinin tepe noktası yoktur. A oyuncusunun A1 stratejisini oynama olasılığına x dersek, A2 stratejisini oynama olasılığı da ( 1 – x ) olur. B oyuncusunun A oyuncusuna yapacağı beklenen ödemeleri veya beklenen değerleri, B’nin tam stratejilerine göre şöyle olacaktır:

Oyunları çözmek için uygun teknikleri geliştirmede kullanılacak iki temel önermeden ikincisine göre, tablonun sağ tarafındaki denklemlerin her biri oyun değeri (v) ye eşit veya ondan daha büyük olmalıdır.

A oyuncusu, amacı kendi gelirini en yükseğe çıkarmak olduğu için, oyunun değerini mümkün olduğu kadar büyük yapacak x olasılığını seçmeye çalışır.

A oyuncusu için problemi doğrusal  programlama problemi olarak aşağıdaki şekilde yazabiliriz:
Maksimum Z = v

Kısıtlayıcılar:
11x – 2 ≥ v
3– 6x ≥ v
5– 9x ≥ v
7x – 1 ≥ v

ve

0 ≤ x ≤ 1

Dikkat edilirse v için negatif olmama koşulu yoktur. Elimizde x ve v gibi iki karar değişkeni bulunduğundan, problemi grafik yöntemiyle çözebiliriz. Alışılmış olarak v dikey eksende, x de yatay eksende gösterilir. Problemdeki son kısıtlayıcı yüzünden x sadece 0 ile 1 aralığı içinde  yer alır. Grafik çözüm tekniğine göre x ve v  değerlerini elde edelim:

11x – 2 = v  denkleminde,
x = 0  için  v = -2
x = 1  için  v =  9
v = 0  için  x = 2 / 11 dir.

3– 6x = v  denkleminde,
x = 0  için  v = 3
x = 1  için  v =  -3
v = 0  için  x = 1 /  2 dir.

5– 9x = v  denkleminde,
x = 0  için  v = 5
x = 1  için  v =  -4
v = 0  için  x =  5 / 9 dur.

7x – 1 = v  denkleminde,
x = 0  için  v = -1
x = 1  için  v =  6
v = 0  için  x =  1 / 7

Şimdi bu değerleri yerlerine koyarak grafiğimizi çizelim.

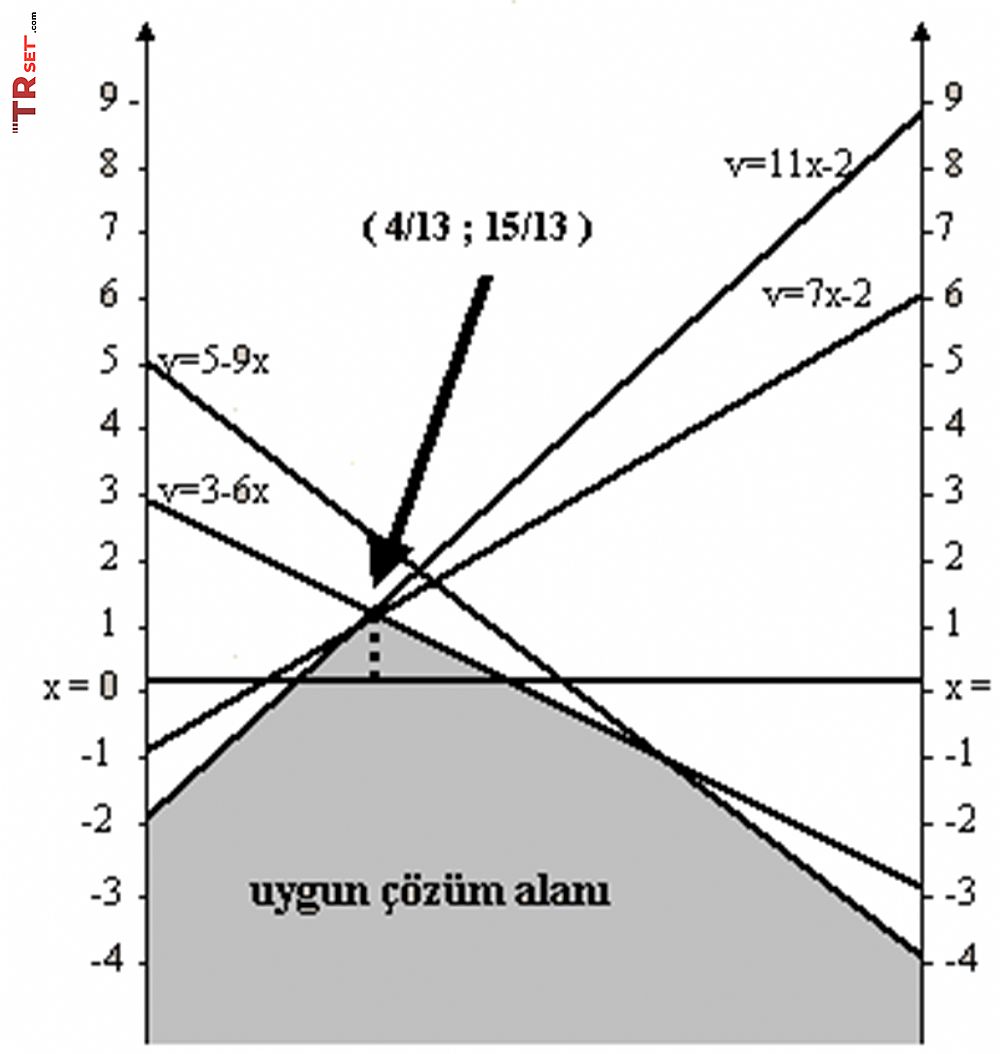
Uygun çözüm alanındaki maksimum kazancı verecek x in optimal değerini bulmak için;
v =  3 – 6x
v = 7x – 1  denklemlerinden yararlanılır.
3 – 6x = 7x – 1     13x = 4    v = 15 / 13 dür.

Şekildeki taralı alanın en yüksek noktası  (4/13 , 15/13) dir. Böylece oyunun değeri  v= 15/13, x’in optimal değeri de  x* = 4/13  dir. A oyuncusunun optimal strateji vektörü,
x*=(4/13 , 9/13) olur.

Grafikte de görüldüğü gibi, maksimum yani en yüksek noktadan iki doğru geçer ki, bunlar da B oyuncusunun B2 tam stratejisine, v = 7x – 1 doğrusu da B4 stratejisine karşılıktır. Bu demektir ki, B oyuncusunun optimal stratejisi sadece B2 ve B4 stratejilerinin karması olacaktır. Geriye kalan B1 ve B3 stratejileri hiçbir zaman oynanmayacaktır. 2xn oyunlarında bir genelleme için şunu söyleyebiliriz. Maksimum noktadan geçmeyen doğruların stratejileri hiçbir zaman oynanmamalıdır. Böylece örneğimizde  y1 = y3 = 0  olur. Eğer A oyuncusu A1 stratejisini oynarsa A ya beklenen ödeme;  9y1 - 3y2 - 4y3 + 6y4  olur. Eğer A oyuncusu A2 stratejisini oynarsa A ya beklenen ödeme   -2y1 + 3y2 + 5y3 – y4   olur. Aynı zamanda bu denklemler oyunun değerine eşit olmalıdır. Öyleyse,

9y1 - 3y2 - 4y3 + 6y4 = v
-2y1 + 3y2 + 5y3 – y4 = v

ve y1 = y3 = 0  olduğundan

-3y2+ 6y4 = 15 / 13
-3y2 – y4 = 15 / 13

Bu denklemim çözümü de bize
y4 = 6 / 13     y2  = 7 / 13   verir.

Aynı zamanda bu değerler B oyuncusunun optimal strateji vektörünün değerleri olur. Buna göre B oyuncusunun optimal strateji vektörü:


y * =     ( 0 ,  7 / 13 ,   0 ,   6 / 13 )  dir.

Bugünün dünyasında, çok hızlı değişim ve gelişim içerisindedir. Böyle bir ortamda işletmeler ayakta kalabilmeleri, yapacakları iç ve dış işletme analizlerine ve bu analizler ışığında alınacak kararlara bağlıdır.

Karar alma tekniklerinden biri de oyun teorisidir. Oyun teorisini tarihsel gelişimi irdelendiğinde, oyunların şans kuramı 17. Yüzyılda ortaya atılmış ve olasılık kuramı adı verilen matematik dalının gelişmesinde kaynak olduğu görülür. Çıkarları çatışan tarafların akılcı davranış kurallarının belirlenmesi olan oyun teorisi, bu tür karar ortamlarını açıklayan matematiksel bir yaklaşımdır.

Kaynaklar :

* Cinemre, Nalan; Yöneylem Araştırması, Beta Basım Yayım Dağıtım A.Ş., İstanbul, 1997.
* Friedman, James W.; Game Theory With Applications To Economics, 2nd ed., Oxford University Press, New York, 1990.
* Fudenberg, Drew and Jean Tirole; Game Theory, The MIT Press, Massachusetts, 1998.
* Halaç, Osman; Kantitatif Karar Verme Teknikleri (Yöneylem Araştırması), 4.b., Alfa Basım Yayım Dağıtım, İstanbul, 1995.
* Hodgetts, Richard M.; Yönetim, 2.b., çev. Canan Çetin, Esin (Can) Mutlu, Beta, İstanbul, 1999.
* Öztürk, Ahmet; Yöneylem Araştırması, 5.b., Ekin Kitapevi Yayınları, Bursa, 1997.
* Romp, Graham; Game Theory-Introduction and Applications, Oxford University Press, Great Britain, 1997.